Replicating the Gurkaynak, Sack, and Wright (2006) Treasury Yield Curve

Replicating the Gurkaynak, Sack, and Wright (2006) Treasury Yield Curve#

Introduction#

In this section, we’ll explore how to replicate the U.S. Treasury yield curve estimation methodology developed by Gurkaynak, Sack, and Wright (2006) (hereafter GSW). The GSW yield curve has become a standard benchmark in both academic research and industry practice. Their approach provides daily estimates of the U.S. Treasury yield curve from 1961 to the present, making it an invaluable resource for analyzing historical interest rate dynamics.

The Nelson-Siegel-Svensson Model#

The GSW methodology employs the Nelson-Siegel-Svensson (NSS) model to fit the yield curve. The NSS model expresses instantaneous forward rates using a flexible functional form with six parameters:

Example: NSS Forward Rate Function The instantaneous forward rate n years ahead is given by:

\[ f(n) = \beta_1 + \beta_2 e^{-n/\tau_1} + \beta_3\left(\frac{n}{\tau_1}\right)e^{-n/\tau_1} + \beta_4\left(\frac{n}{\tau_2}\right)e^{-n/\tau_2} \]

This specification allows for rich curve shapes while maintaining smoothness and asymptotic behavior. The parameters have intuitive interpretations:

  • \(\beta_1\): The asymptotic forward rate

  • \(\beta_2\), \(\beta_3\), \(\beta_4\): Control the shape and humps of the curve

  • \(\tau_1\), \(\tau_2\): Determine the location of curve features

\[ y(t) = \beta_1 + \beta_2\left(\frac{1-e^{-t/\tau_1}}{t/\tau_1}\right) + \beta_3\left(\frac{1-e^{-t/\tau_1}}{t/\tau_1} - e^{-t/\tau_1}\right) + \beta_4\left(\frac{1-e^{-t/\tau_2}}{t/\tau_2} - e^{-t/\tau_2}\right) \]

This equation shows the zero-coupon yield \(y(t)\) for maturity \(t\).

import os
from datetime import datetime
from pathlib import Path

import numpy as np
import pandas as pd
from dotenv import load_dotenv

import finm

load_dotenv()

DATA_DIR = Path(os.environ.get("DATA_DIR", "./_data"))
DATA_DIR.mkdir(parents=True, exist_ok=True)
WRDS_USERNAME = os.environ.get("WRDS_USERNAME", "")

# Nelson-Siegel-Svensson parameters
# "tau1", "tau2", "beta1", "beta2", "beta3", "beta4"
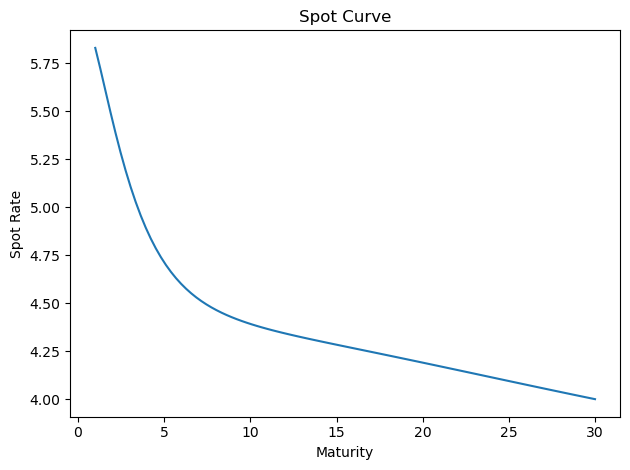
params = np.array([1.0, 10.0, 3.0, 3.0, 3.0, 3.0])

finm.plot_spot_curve(params)
../_images/ed8ff83f8de2a5ddeb29600f4db0ea0c9bd99c1f5066983b8cce7f248dc96168.png 
<Axes: title={'center': 'Spot Curve'}, xlabel='Maturity', ylabel='Spot Rate'>

# Nelson-Siegel-Svensson parameters
# "tau1", "tau2", "beta1", "beta2", "beta3", "beta4"
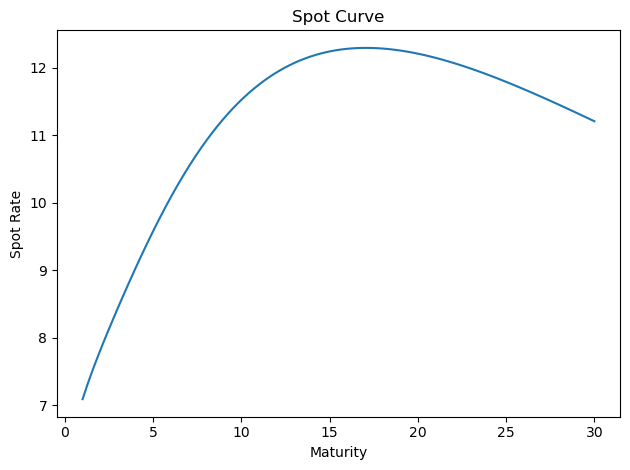
params = np.array([1.0, 10.0, 3.0, 3.0, 3.0, 30.0])

finm.plot_spot_curve(params)
../_images/c7c3b005c6391cd0dd32c24bc46df53ddae416c3189d7c8da01ad89421761466.png 
<Axes: title={'center': 'Spot Curve'}, xlabel='Maturity', ylabel='Spot Rate'>

Theoretical Foundations#

The Nelson-Siegel-Svensson model is commonly used in practice to fit the yield curve. It has statistically appealing properties, but it is not arbitrage-free. Here’s a detailed breakdown of why:

1. Static Curve-Fitting Approach#

  • The NSS model is primarily a parametric curve-fitting tool that focuses on matching observed yields at a single point in time.

  • It does not model the dynamic evolution of interest rates or enforce consistency between short-term rate expectations and long-term yields over time, a key requirement for no-arbitrage models.

2. Absence of No-Arbitrage Restrictions#

  • No-arbitrage models impose constraints to prevent risk-free profits. For example, affine term structure models derive bond prices from:

    \[ P(t,T) = \mathbb{E}^\mathbb{Q}\left[e^{-\int_t^T r_s ds}\right], \]

    where \(\mathbb{Q}\) is the risk-neutral measure. The NSS model lacks such theoretical foundations.

  • The NSS parameters (e.g., level, slope, curvature) are statistically estimated rather than derived from economic principles or arbitrage-free dynamics.

3. Factor Dynamics and Risk Premiums#

  • In arbitrage-free models, factor dynamics (e.g., mean reversion) and risk premiums are explicitly defined to ensure consistency across maturities. The NSS model treats factors as latent variables without specifying their stochastic behavior or market price of risk.

  • This omission allows potential inconsistencies between short-rate expectations and long-term yields, creating theoretical arbitrage opportunities.

4. Contrast with Arbitrage-Free Extensions#

  • The arbitrage-free Nelson-Siegel (AFNS) model, developed by Christensen et al. (2007), addresses these limitations by:

    • Embedding Nelson-Siegel factors into a dynamic arbitrage-free framework.

    • Explicitly defining factor dynamics under both physical (\(\mathbb{P}\)) and risk-neutral (\(\mathbb{Q}\)) measures.

    • Ensuring internal consistency between yields of different maturities.

5. Empirical vs. Theoretical Focus#

  • The NSS model prioritizes empirical flexibility (e.g., fitting yield curve shapes like humps) over theoretical rigor. While it performs well in practice, this trade-off inherently sacrifices no-arbitrage guarantees.

In summary, the NSS model’s lack of dynamic factor specifications, absence of explicit no-arbitrage constraints, and focus on cross-sectional fitting rather than intertemporal consistency render it theoretically incompatible with arbitrage-free principles. Its successors, such as the AFNS model, bridge this gap by integrating no-arbitrage restrictions while retaining empirical tractability.

Data Filtering#

One important step of the GSW methodology is careful filtering of Treasury securities.

The following filters are implemented:

  1. Exclude securities with < 3 months to maturity

  2. Exclude on-the-run and first off-the-run issues after 1980

  3. Exclude T-bills (only keep notes and bonds)

  4. Exclude 20-year bonds after 1996 with decay

  5. Exclude callable bonds

The GSW paper also includes ad hoc exclusions for specific issues, which are not implemented here.

Why are these filters important?

For (2), this is what the paper says:

We exclude the two most recently issued securities with maturities of two, three, four, five, seven, ten, twenty, and thirty years for securities issued in 1980 or later. These are the “on-the-run” and “first off-the-run” issues that often trade at a premium to other Treasury securities, owing to their greater liquidity and their frequent specialness in the repo market. Earlier in the sample, the concept of an on-the-run issue was not well defined, since the Treasury did not conduct regular auctions and the repo market was not well developed (as discussed by Garbade (2004)). Our cut-off point for excluding on-the-run and first off-the-run issues is somewhat arbitrary but is a conservative choice (in the sense of potentially erring on the side of being too early).

For (4), this is what the paper says:

We begin to exclude twenty-year bonds in 1996, because those securities often appeared cheap relative to ten-year notes with comparable duration. This cheapness could reflect their lower liquidity or the fact that their high coupon rates made them unattractive to hold for tax-related reasons.

To avoid an abrupt change to the sample, we allow their weights to linearly decay from 1 to 0 over the year ending on January 2, 1996.

Let’s examine how this affects the data.

# Load Gurkaynak Sack Wright data from Federal Reserve's website
# See here: https://www.federalreserve.gov/data/nominal-yield-curve.htm
# and here: https://www.federalreserve.gov/data/yield-curve-tables/feds200628_1.html
# Auto-pulls data if not found locally

actual_all = finm.load_fed_yield_curve_all(
    data_dir=DATA_DIR,
    pull_if_not_found=True,
    accept_license=True,
).to_pandas()
actual_all = actual_all.set_index("Date")

# Create copy of parameter DataFrame to avoid view vs copy issues
actual_params_all = actual_all.loc[
    :, ["TAU1", "TAU2", "BETA0", "BETA1", "BETA2", "BETA3"]
].copy()

# Convert percentage points to decimals for beta parameters
beta_columns = ["BETA0", "BETA1", "BETA2", "BETA3"]
actual_params_all[beta_columns] = actual_params_all[beta_columns] / 100

# Load CRSP Treasury data from Wharton Research Data Services
# We will fit a Nelson-Siegel-Svensson model to this data to see
# if we can replicate the Gurkaynak Sack Wright results above.
# Auto-pulls from WRDS if not found locally (requires WRDS credentials).
df_all = finm.load_wrds_treasury(
    data_dir=DATA_DIR,
    variant="consolidated",
    with_runness=True,
    pull_if_not_found=True,
    wrds_username=WRDS_USERNAME,
    start_date="1970-01-01",
    end_date=datetime.today().strftime("%Y-%m-%d"),
).to_pandas()

df_all.tail()
kytreasno kycrspid tcusip caldt tdatdt tmatdt tfcaldt tdbid tdask tdaccint ... tdpdint tcouprt itype original_maturity years_to_maturity tdduratn tdretnua days_to_maturity callable run
2522871 208490.0 20551115.104630 912810UP 2025-11-21 2025-11-15 2055-11-15 1970-01-01 98.578125 98.593750 0.076657 ... 0.0 4.625 1.0 30.0 30.0 5987.545832 0.002352 10951 False 0
2522872 208490.0 20551115.104630 912810UP 2025-11-24 2025-11-15 2055-11-15 1970-01-01 99.125000 99.140625 0.114986 ... 0.0 4.625 1.0 30.0 30.0 5998.448559 0.005931 10948 False 0
2522873 208490.0 20551115.104630 912810UP 2025-11-25 2025-11-15 2055-11-15 1970-01-01 99.390625 99.406250 0.127762 ... 0.0 4.625 1.0 30.0 30.0 6004.161566 0.002805 10947 False 0
2522874 208490.0 20551115.104630 912810UP 2025-11-26 2025-11-15 2055-11-15 1970-01-01 99.781250 99.796875 0.140539 ... 0.0 4.625 1.0 30.0 30.0 6012.986729 0.004053 10946 False 0
2522875 208490.0 20551115.104630 912810UP 2025-11-28 2025-11-15 2055-11-15 1970-01-01 99.359375 99.375000 0.166091 ... 0.0 4.625 1.0 30.0 30.0 6000.389794 -0.003966 10944 False 0

5 rows × 24 columns

df_all.describe()
kytreasno caldt tdatdt tmatdt tfcaldt tdbid tdask tdaccint tdyld price ... tdtotout tdpdint tcouprt itype original_maturity years_to_maturity tdduratn tdretnua days_to_maturity run
count 2.522876e+06 2522876 2522876 2522876 2522876 2.522832e+06 2.522832e+06 2.522876e+06 2.522832e+06 2.522832e+06 ... 2.500507e+06 2.522876e+06 2.522876e+06 2.522876e+06 2.522876e+06 2.522876e+06 2.522876e+06 2.520799e+06 2.522876e+06 2.522876e+06
mean 2.045723e+05 2005-01-15 02:42:02.172948992 2000-03-12 20:42:25.357917056 2011-04-03 21:33:24.438109440 1970-01-01 00:00:00 1.043663e+02 1.044508e+02 1.338581e+00 1.204765e-04 1.057471e+02 ... 2.504440e+04 1.966721e-02 5.378773e+00 1.747345e+00 1.104796e+01 6.219792e+00 1.656792e+03 2.019265e-04 2.269786e+03 1.916606e+01
min 2.006360e+05 1970-01-02 00:00:00 1955-02-15 00:00:00 1970-02-15 00:00:00 1970-01-01 00:00:00 4.350000e+01 4.354688e+01 0.000000e+00 -1.664162e-02 4.405673e+01 ... 4.000000e+00 0.000000e+00 1.250000e-01 1.000000e+00 1.000000e+00 0.000000e+00 -1.000000e+00 -1.094112e-01 1.000000e+00 0.000000e+00
25% 2.028470e+05 1992-08-31 00:00:00 1987-05-15 00:00:00 1997-04-15 00:00:00 1970-01-01 00:00:00 9.899219e+01 9.906250e+01 3.505435e-01 4.855124e-05 9.980185e+01 ... 8.914000e+03 0.000000e+00 2.375000e+00 1.000000e+00 5.000000e+00 1.000000e+00 5.115154e+02 -5.799535e-04 5.280000e+02 5.000000e+00
50% 2.040580e+05 2008-04-29 00:00:00 2000-02-15 00:00:00 2015-02-15 00:00:00 1970-01-01 00:00:00 1.009336e+02 1.009922e+02 9.079484e-01 1.152282e-04 1.022988e+02 ... 1.925100e+04 0.000000e+00 4.750000e+00 2.000000e+00 7.000000e+00 3.000000e+00 1.113495e+03 1.454466e-04 1.213000e+03 1.400000e+01
75% 2.066810e+05 2018-03-05 00:00:00 2013-11-15 00:00:00 2023-04-30 00:00:00 1970-01-01 00:00:00 1.064609e+02 1.065312e+02 1.973412e+00 1.714633e-04 1.082203e+02 ... 3.521200e+04 0.000000e+00 7.875000e+00 2.000000e+00 1.000000e+01 7.000000e+00 2.163618e+03 1.028578e-03 2.548000e+03 2.800000e+01
max 2.084900e+05 2025-11-28 00:00:00 2025-11-30 00:00:00 2055-11-15 00:00:00 1970-01-01 00:00:00 1.763281e+02 1.763906e+02 1.186908e+01 6.557793e-03 1.827193e+02 ... 1.485010e+05 1.191304e+01 1.625000e+01 2.000000e+00 4.000000e+01 3.000000e+01 9.160067e+03 1.281108e-01 1.105300e+04 8.400000e+01
std 2.074286e+03 NaN NaN NaN NaN 1.312852e+01 1.310968e+01 1.296819e+00 8.754251e-05 1.350790e+01 ... 2.128712e+04 2.762166e-01 3.560476e+00 4.345348e-01 9.982702e+00 7.413479e+00 1.638129e+03 3.687852e-03 2.701602e+03 1.794348e+01

8 rows × 21 columns

df_all = finm.gurkaynak_sack_wright_filters(df_all)
df_all.describe()
kytreasno caldt tdatdt tmatdt tfcaldt tdbid tdask tdaccint tdyld price ... tdpdint tcouprt itype original_maturity years_to_maturity tdduratn tdretnua days_to_maturity run weight
count 2.114163e+06 2114163 2114163 2114163 2114163 2.114157e+06 2.114157e+06 2.114163e+06 2.114157e+06 2.114157e+06 ... 2.114163e+06 2.114163e+06 2.114163e+06 2.114163e+06 2.114163e+06 2.114163e+06 2.113977e+06 2.114163e+06 2.114163e+06 2.114163e+06
mean 2.046198e+05 2005-07-19 15:52:12.356210048 2000-08-16 09:24:55.980962688 2011-08-31 22:56:37.221879808 1970-01-01 00:00:00 1.047623e+02 1.048439e+02 1.299545e+00 1.171018e-04 1.061026e+02 ... 2.082902e-02 5.246122e+00 1.760005e+00 1.102895e+01 6.122262e+00 1.650046e+03 1.977330e-04 2.234295e+03 2.102501e+01 9.992381e-01
min 2.006560e+05 1970-01-02 00:00:00 1955-02-15 00:00:00 1970-05-15 00:00:00 1970-01-01 00:00:00 4.350000e+01 4.354688e+01 0.000000e+00 -4.305986e-05 4.405673e+01 ... 0.000000e+00 1.250000e-01 1.000000e+00 1.000000e+00 0.000000e+00 -1.000000e+00 -1.094112e-01 9.300000e+01 0.000000e+00 1.095890e-02
25% 2.028900e+05 1993-03-15 00:00:00 1988-03-03 00:00:00 1997-09-30 00:00:00 1970-01-01 00:00:00 9.890625e+01 9.896875e+01 3.483607e-01 4.588084e-05 9.977082e+01 ... 0.000000e+00 2.250000e+00 2.000000e+00 5.000000e+00 1.000000e+00 5.222422e+02 -5.841185e-04 5.420000e+02 8.000000e+00 1.000000e+00
50% 2.040690e+05 2009-09-25 00:00:00 2002-08-31 00:00:00 2016-01-31 00:00:00 1970-01-01 00:00:00 1.013125e+02 1.013750e+02 8.888122e-01 1.116832e-04 1.025494e+02 ... 0.000000e+00 4.625000e+00 2.000000e+00 7.000000e+00 3.000000e+00 1.114798e+03 1.457781e-04 1.205000e+03 1.600000e+01 1.000000e+00
75% 2.066990e+05 2018-06-27 00:00:00 2014-01-31 00:00:00 2023-06-30 00:00:00 1970-01-01 00:00:00 1.070625e+02 1.071250e+02 1.906250e+00 1.686799e-04 1.088083e+02 ... 0.000000e+00 7.750000e+00 2.000000e+00 1.000000e+01 7.000000e+00 2.102027e+03 1.016264e-03 2.444000e+03 3.000000e+01 1.000000e+00
max 2.084450e+05 2025-11-28 00:00:00 2025-08-31 00:00:00 2055-02-15 00:00:00 1970-01-01 00:00:00 1.763281e+02 1.763906e+02 1.186908e+01 9.394247e-04 1.827193e+02 ... 1.191304e+01 1.625000e+01 2.000000e+00 4.000000e+01 2.900000e+01 8.738464e+03 1.281108e-01 1.069200e+04 8.300000e+01 1.000000e+00
std 2.072288e+03 NaN NaN NaN NaN 1.342110e+01 1.340406e+01 1.249766e+00 8.423687e-05 1.379275e+01 ... 2.796795e-01 3.473341e+00 4.270803e-01 9.938899e+00 7.221291e+00 1.610957e+03 3.591343e-03 2.632977e+03 1.746867e+01 2.241824e-02

8 rows × 22 columns

Implementation Steps#

1. Data Preparation#

First, we load and clean the CRSP Treasury data

# Data was already loaded above with pull_if_not_found=True
# Just reload with filters if needed
df_all = finm.load_wrds_treasury(
    data_dir=DATA_DIR,
    variant="consolidated",
    with_runness=True,
).to_pandas()

2. Cashflow Construction#

For each Treasury security, we need to calculate its future cashflows. Consider the following simplified example:

sample_data = pd.DataFrame(
    {
        "tcusip": ["A", "B", "C", "D", "E"],
        "tmatdt": pd.to_datetime(
            ["2000-05-15", "2000-05-31", "2000-06-30", "2000-07-31", "2000-08-15"]
        ),
        "price": [101, 101, 100, 100, 103],
        "tcouprt": [6, 6, 0, 5, 6],
        "caldt": pd.to_datetime("2000-01-31"),
    }
)

cashflow = finm.calc_cashflows(sample_data)

# Treasury securities have 2 coupon payments per year
# and pay their final coupon and principal on the maturity date
expected_cashflow = np.array(
    [
        [0.0, 103.0, 0.0, 0.0, 0.0, 0.0],
        [0.0, 0.0, 103.0, 0.0, 0.0, 0.0],
        [0.0, 0.0, 0.0, 100.0, 0.0, 0.0],
        [0.0, 0.0, 0.0, 0.0, 102.5, 0.0],
        [3.0, 0.0, 0.0, 0.0, 0.0, 103.0],
    ]
)

cashflow
2000-02-15 2000-05-15 2000-05-31 2000-06-30 2000-07-31 2000-08-15
0 0.0 103.0 0.0 0.0 0.0 0.0
1 0.0 0.0 103.0 0.0 0.0 0.0
2 0.0 0.0 0.0 100.0 0.0 0.0
3 0.0 0.0 0.0 0.0 102.5 0.0
4 3.0 0.0 0.0 0.0 0.0 103.0

3. Model Fitting#

The NSS model is fit by minimizing price errors weighted by duration:

\[ \min_{\beta,\tau} \sum_{i=1}^N \frac{(P_i^{obs} - P_i^{model})^2}{D_i} \]

where:

  • \(P_i^{obs}\) = Observed clean price (including accrued interest)

  • \(P_i^{model}\) = Model-implied price

  • \(D_i\) = Duration of security i

Now, why are the squared errors weighted by the duration?

Recall that bond duration is a measurement of how much a bond’s price will change in response to interest rate changes. Thus, the price error objective is approximately equivalent to minimizing unweighted yield errors:

\[ \frac{(P_i^{obs} - P_i^{model})^2}{D_i} \approx D_i \cdot (y_i^{obs} - y_i^{model})^2 \]

This approximation comes from the duration relationship: $\( P^{obs} - P^{model} \approx -D \cdot (y^{obs} - y^{model}) \)$

Making the objective function: $\( \sum D_i \cdot (y_i^{obs} - y_i^{model})^2 \)$

So, why Price Errors Instead of Yield Errors?

  1. Non-linear relationship: The price/yield relationship is convex (convexity adjustment matters more for long-duration bonds)

  2. Coupon effects: Directly accounts for differential cash flow timing

  3. Numerical stability: Prices have linear sensitivity to parameters via discount factors, while yields require non-linear root-finding

  4. Economic meaning: Aligns with trader behavior that thinks in terms of price arbitrage

Reference: Gurkaynak, Sack, and Wright (2006)

Testing and Validation#

To validate our implementation, we compare our fitted yields against the official GSW yields published by the Federal Reserve:

# Load Gurkaynak Sack Wright data from Federal Reserve's website (already cached)
actual_all = finm.load_fed_yield_curve_all(data_dir=DATA_DIR).to_pandas()
actual_all = actual_all.set_index("Date")
# Create copy of parameter DataFrame to avoid view vs copy issues
actual_params_all = actual_all.loc[
    :, ["TAU1", "TAU2", "BETA0", "BETA1", "BETA2", "BETA3"]
].copy()
# Convert percentage points to decimals for beta parameters
beta_columns = ["BETA0", "BETA1", "BETA2", "BETA3"]
actual_params_all[beta_columns] = actual_params_all[beta_columns] / 100


# Load CRSP Treasury data from local cache (already pulled above)
df_all = finm.load_wrds_treasury(
    data_dir=DATA_DIR,
    variant="consolidated",
    with_runness=True,
).to_pandas()
df_all = finm.gurkaynak_sack_wright_filters(df_all)

quote_dates = pd.date_range("2000-01-02", "2024-06-30", freq="BMS")

Test Day 1#

# Test Day 1
quote_date = pd.to_datetime("2024-06-03")
# Subset df_all to quote_date
df = df_all[df_all["caldt"] == quote_date]
actual_params = actual_params_all[actual_params_all.index == quote_date].values[0]

# "tau1", "tau2", "beta1", "beta2", "beta3", "beta4"
params0 = np.array([0.989721, 9.955324, 3.685087, 1.579927, 3.637107, 9.814584])

params_star, error = finm.fit(quote_date, df_all, params0)

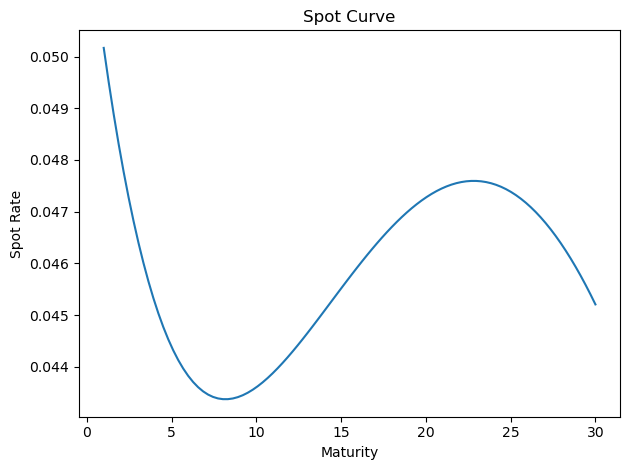
# Visualize the fit
finm.plot_spot_curve(params_star)
../_images/0b68ca1597dbd812dd86e7d1fec2d8e6dd6c87c7a56b70ee6ecd07c24656a373.png 
<Axes: title={'center': 'Spot Curve'}, xlabel='Maturity', ylabel='Spot Rate'>

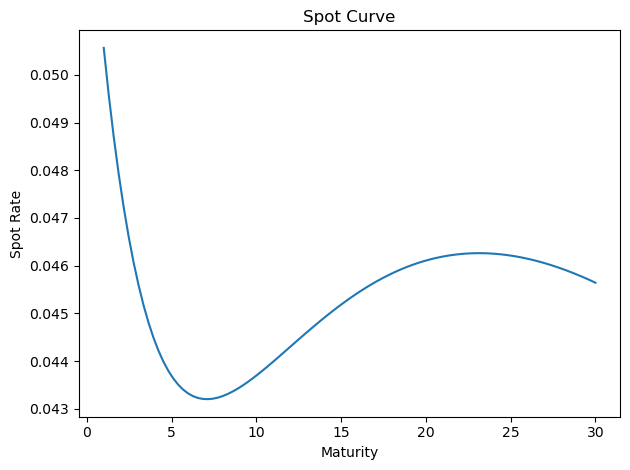
finm.plot_spot_curve(actual_params)
../_images/65b05e37390dd0932f49708c60f8b184bebb4222d2ba42c98ffb3b09603025c1.png 
<Axes: title={'center': 'Spot Curve'}, xlabel='Maturity', ylabel='Spot Rate'>

price_comparison = finm.compare_fit(quote_date, df_all, params_star, actual_params, df)
price_comparison
Actual Price GSW Predicted Price Model Predicted Price Predicted - Actual % Predicted - GSW %
tcusip
912810ET 104.189560 103.877734 103.934239 -0.002451 0.000544
912810EV 104.504035 104.146501 104.169835 -0.003198 0.000224
912810EW 103.835766 103.539602 103.500204 -0.003232 -0.000381
912810EX 106.232229 106.071133 105.960397 -0.002559 -0.001044
912810EY 105.202785 104.356538 104.209598 -0.009441 -0.001408
... ... ... ... ... ...
91282CJW 99.132169 99.440209 99.129604 -0.000026 -0.003124
91282CJX 98.413419 99.124083 98.902013 0.004965 -0.002240
91282CKB 100.744735 100.757545 100.712789 -0.000317 -0.000444
91282CKD 99.929178 100.242964 99.930621 0.000014 -0.003116
91282CKC 100.226053 100.302116 100.083359 -0.001424 -0.002181

292 rows × 5 columns

# Assert that column is close to 0 for all CUSIPs
assert (price_comparison["Predicted - Actual %"].abs() < 0.05).all()
assert (price_comparison["Predicted - GSW %"].abs() < 0.02).all()

Test Day 2#

# Test Day 2
quote_date = pd.to_datetime("2000-06-05")
# Subset df_all to quote_date
df = df_all[df_all["caldt"] == quote_date]
actual_params = actual_params_all[actual_params_all.index == quote_date].values[0]

params0 = np.array([0.989721, 9.955324, 3.685087, 1.579927, 3.637107, 9.814584])

params_star, error = finm.fit(quote_date, df_all, params0)

price_comparison = finm.compare_fit(quote_date, df_all, params_star, actual_params, df)

# Assert that column is close to 0 for all CUSIPs
assert (price_comparison["Predicted - Actual %"].abs() < 0.05).all()
assert (price_comparison["Predicted - GSW %"].abs() < 0.02).all()

Test Day 3#

# Test Day 3
quote_date = pd.to_datetime("1990-06-05")
# Subset df_all to quote_date
df = df_all[df_all["caldt"] == quote_date]
actual_params = actual_params_all[actual_params_all.index == quote_date].values[0]

params0 = np.array([0.989721, 9.955324, 3.685087, 1.579927, 3.637107, 9.814584])

params_star, error = finm.fit(quote_date, df_all, params0)

price_comparison = finm.compare_fit(quote_date, df_all, params_star, actual_params, df)

# Assert that column is close to 0 for all CUSIPs
assert (price_comparison["Predicted - Actual %"].abs() < 0.05).all()
assert (price_comparison["Predicted - GSW %"].abs() < 0.02).all()

Conclusion#

The GSW yield curve methodology provides a robust framework for estimating the U.S. Treasury yield curve. By carefully implementing their filtering criteria and optimization approach, we can replicate their results with high accuracy. This implementation allows us to extend their analysis to current data and provides a foundation for various fixed-income applications.

Example: Model Performance Our implementation typically achieves price errors below 0.02% compared to the official GSW yields, demonstrating the reliability of the replication.

Contents